Our Mythical Childhood...

30.12.2024

Anna Łukomska – nauczycielka matematyki w LO "Strumienie"

Matematyczne modele walki Heraklesa z Hydrą lernejską

Dzięki współpracy nauczycieli i uczennic w interdyscyplinarnym projekcie Cum Heracle ad fontes properamus* mitologia stała się dla mnie i moich uczennic źródłem inspiracji na lekcjach matematyki. Przeczytałyśmy wspólnie mit o Heraklesie opisany w Mitologii przez Jana Parandowskiego. Zainteresowała nas szczególnie walka Heraklesa z Hydrą lernejską.

Walka Heraklesa z Hydrą, malowały uczennice klasy VII Szkoły Podstawowej „Strumienie”. 

Uznałyśmy, że jest to historia, na podstawie której możemy zbudować modele dwóch walk Heraklesa z Hydrą, odwołując się do wiedzy i umiejętności wypracowanych dotąd na lekcjach matematyki:

• pojęcia funkcji, 
• umiejętności rysowania wykresu funkcji dyskretnej,
• stosowania grafu jako schematu rysunku,
• podstawy programowania w Pythonie.

I. Cele lekcji: 

• formułowanie pytań inspirowanych mitem o Heraklesie, przydatnych do analizy matematycznej,
• poznanie pojęcia fraktal i określenie własności fraktali na podstawie najprostszego modelu – grafu drzewa,
• zastosowania grafów, funkcji do matematycznego modelowania sytuacji życiowych,
• zbudowanie matematycznego modelu dwóch walk Heraklesa z Hydrą (graf, liczba głów Hydry jako funkcja liczby cięć – wzór, wykres) oraz innych (wymyślonych) scenariuszy, 
• ćwiczenia analizy i syntezy danych (obserwacja stanów walki i opis tych stanów ogólnym wzorem), dopasowanie funkcji do scenariusza,
• analiza kodu realizującego w Pythonie grafy Hydry (definicja rekurencyjna).

II. Zadania uczniów:

Część 1. Czytanie i analiza fragmentu mitu o Heraklesie i Hydrze (według Mitologii Jana Parandowskiego) 

„Teraz (Eurysteus) polecił mu zabić hydrę lernejską. Koło miejscowości Lerna, niedaleko Argos, rozlewały się szerokie bagniska otoczone ze wszech stron skałami. Brzegiem owych bagien przemykała się wąska ścieżka, którą musiał przejść każdy, kto zdążał z Argolidy do Lakonii. Tam właśnie osiadł ów płaz ohydny i czyhał na ludzi. Gdy mu zabrakło pożywienia, zapuszczał się między wsie okoliczne, rozszarpywał bydło i niszczył plony. Hydra była niezmiernie wielka i miała dziesięć głów, z których jedną, w samym środku, nieśmiertelną. Herakles przyjechawszy do Lerny zatrzymał konie i zaczął strzelać w głąb smoczej jamy. Rozjuszona bestia opuściła kryjówkę, a wtedy on chwycił ją za gardziel. Macki hydry oplotły się dokoła jego nogi, tak że musiał dobrze uważać, żeby nie upaść. Po długiej walce oberwał jej parę głów, ale to się na nic nie zdało, bo na miejsce jednej uciętej zaraz odrastały trzy nowe. Na pomoc hydrze przywlókł się olbrzymi rak, który Heraklesa boleśnie szczypał po nogach. Bohater rozgniótł go obcasem i kazał swemu woźnicy, Jolaosowi, zapalić pobliski las. Gdy się to stało, Herakles na nowo ucinał hydrze jedną głowę po drugiej, a rany natychmiast wypalał i łby więcej nie odrastały. Na koniec wyrwał jej ową nieśmiertelną głowę, zakopał na polu i przywalił ogromnym głazem. Kadłub zaś rozciął i w żółci potwora zatruł swoje strzały. Wyszedł z tej walki strasznie pokąsany i całe ciało go piekło. Któryś z bogów poradził mu, aby poszukał sobie takiego ziela, które kształtem przypomina hydrę. Herakles znalazł to ziele i ozdrowiał. 

Część 2. Krótka rozmowa z całą klasą o drugiej próbie zgładzenia Hydry, formułowanie pytań 

• Jaka wielkość liczbowa jest przydatna do opisu tego zdarzenia? Od czego zależy? (Funkcja liczby żyjących głów Hydry po n-tym cięciu Heraklesa)
• Jak przedstawić etapy tego zdarzenia – rysunkiem, liczbowo?
• Jaki byłby schemat przedstawiający Hydrę (właściwie jej głowy)?

Część 3. Pracujemy metodą „myślącej klasy” 

Uczniowie na podstawie losowania są przydzieleni do dwuosobowych grup i pracują przy komputerach.

• Zad. 1: Inne niż schematyczny obrazek Hydry sposoby przedstawienia liczby głów Hydry w drugiej próbie [wykres, tabelka, wzór f(n)=10-n]. Podsumowanie z pokazaniem różnych sposobów i odniesieniem do pojęcia funkcji.
• Zad. 2: Przedstawcie podobnie – za pomocą funkcji – pierwszą próbę zgładzenia Hydry przez Heraklesa f(n)= n+1.
• Zad. 3: Hydra ma 32 głowy. Herakles ścina jednocześnie wszystkie głowy Hydry, ale za chwilę połowa z tych ściętych odrasta, o ile ta połowa jest równa co najmniej 1. Przedstawcie tę sytuację. Po ilu cięciach Heraklesa Hydra ginie? .
• Zad. 4: Hydra ma 1 głowę. Jedną sekundę po jej ścięciu wyrastają z dawnej szyi dwie nowe głowy i to samo dzieje się po ich ścięciu.
  • Ile głów ma Hydra po kolejnych ścięciach? Napisz wzór na liczbę głów Hydry po n ścięciach. 
  • Graf – fraktal (określenie własności fraktali).
  • Analiza kodu realizującego w Pythonie schematyczny rysunek Hydry:

Część 4. Praca przy komputerach

Napisanie kodu w Pythonie, obserwacja rysunków Hydry przy różnych parametrach (modyfikacja kodu).

n=1	n=2	n=3	n=4

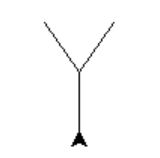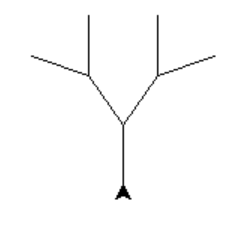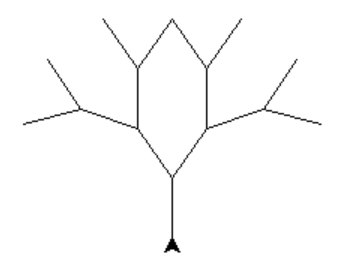III. Podsumowanie 

Podsumowanie w formie rozmowy/dyskusji/wniosków z pracy w grupach :

1. Jaka jest przydatność funkcji jako narzędzia opisującego rzeczywistość?
2. Jaka jest wartość symulacyjnych metod informatycznych?
3. Wyjaśniamy pojęcie fraktal.
4. Uczennice przygotowują informację zwrotną: Co zabierasz ze sobą z tej lekcji, w której matematykę łączymy z mitologią?

*Projekt Cum Heracle ad fontes properamus opisany w dostępnym na stronie programie Ad fontes. Vide także reportaż na temat projektu na kanale YouTube Our Mythical Childhood.